Largest Subarray With Sum 0

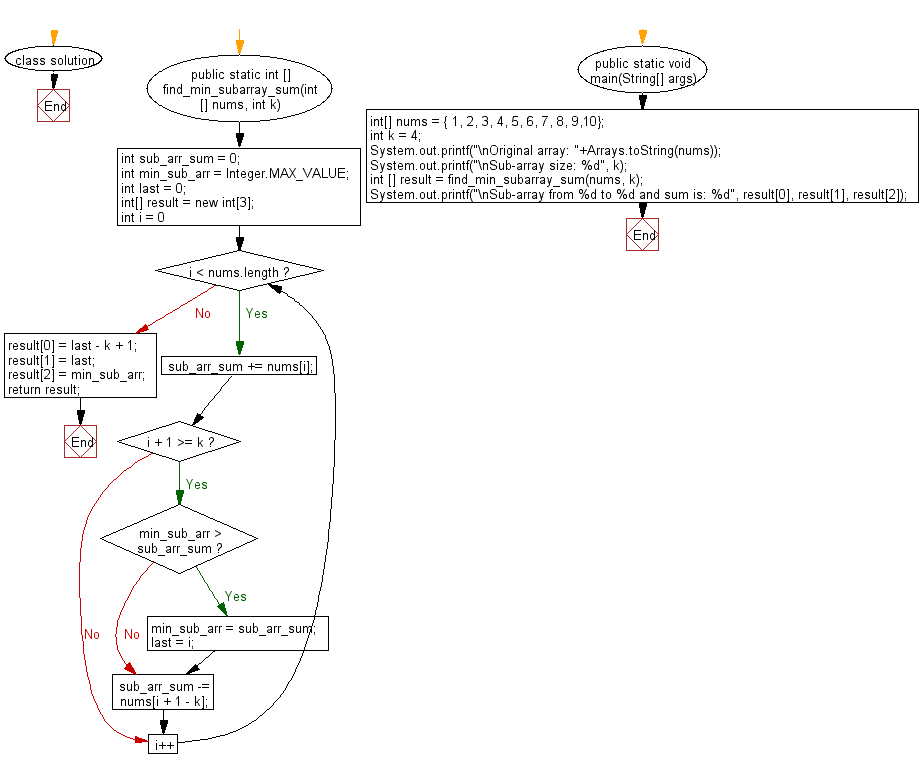
We outlined the max or optimum subarray concern as discovering the utmost sum of some subarray of contiguous values present within the array. On high this, we added an additional stipulation of discovering the utmost sum of non-contiguous elements. Before we might begin, we needed to parse and convert the enter into arrays of integers. For discovering the non-contiguous max sum, we used the foldl or cut back function. For the max subarray problem, we employed a recursive answer protecting monitor of two inputs the place the bottom case was an empty array. Line one is defining this helper perform we have to point out each the max subarray sum and the max sum of non-contiguous elements.

It takes an inventory of integers after which builds a string as output. The the place clauses, commencing on line three, construct up the variables a and b. Cont is the output of max_cont_sum which is the sum of the max subarray.

Ncont is the output of max_ncont_sum which is the utmost sum of the non-contiguous parts within the array. In this article, you may discover ways to seek out the utmost subarray sum. In different words, we have to seek out the contiguous array parts that give us the utmost sum given an array. In every iteration, current_sum is in contrast with max_sum, to replace max_sum whether it's bigger than max_sum. A naive brute pressure strategy can be to calculate the sum of all subarrays of measurement okay of the given array to seek out the utmost sum. An array accommodates equally optimistic and destructive elements, discover the utmost subarray whose sum equals 0.

Given an integer array of N elements, discover the utmost sum contiguous subarray . You can start off off a loop that runs for every index of the array after which for every index you begin yet another loop to add the subsequent okay elements. This way, it's possible for you to to calculate the sum of all k-sized subarrays after which return the utmost of all of the sums. We will first traverse the complete array and keep the current sum. We will look at various if the current sum is supplied within the hash desk or not. If it's current within the hashtable, then replace the utmost measurement of the subarray.

If all array parts are non-negative, then the issue turns into trivial because the utmost subarray sum might be equal to the sum of all array elements. The outer loop picks a place to begin i. The inside loop considers all subarrays ranging from i. If measurement of a subarray is bigger than optimum measurement so far, then replace the utmost size.

A ordinary approach is to make use of two nested loops. Given an array of constructive integers, and a constructive wide variety k, discover the utmost sum of any contiguous subarray of measurement k. For an enter array with solely unfavorable numbers, the past algorithm will return the most important of the integers, which is negative. So this algorithm will return zero, which corresponds to the sum of components of an empty subarray. The time complexity of the above code is O the place N is the variety of components within the array. This is simply because we're traversing the array and simply calculating the sum and storing the sum-index pair within the hashmap.

The notion is to keep the sum of all of the subarrays ranging from the beginning. From that, if any of the values repeat itself, let's say sum until i index and sum until j index is same, it signifies that the sum of parts within the subarray A[i+1…..j] is 0. Moreover, if the sum any index i is 0, then the subarray A[0…i] has sum of its parts equal to 0. Takes two parameters and outputs acc + x if x is optimistic in any different case it simply outputs acc. This operate known as for each aspect within the array. The accumulator acc holds the output from the final time our nameless operate was called.

If we solely ever accumulate or sum up optimistic numbers you may see how this will likely discover the utmost sum of all the non-contiguous components within the array. And if there are not any optimistic components within the array, the acc will solely ever maintain that first zero we exceeded to foldl. WAP in Java to search out the most important subarray with sum zero .

If there's multiple subarray with the most important length, return the subarray with the bottom establishing index.If there's no such thing as a such sub-array return -1. Take the integer array as an enter from the user. WAP in Java to search out the most important subarray with sum 0.

If there's multiple subarray with the most important length, return the subarray with the bottom establishing index.lf there isn't a such sub-array return -1. For all different cases, there's at the least one nonnegative integer within the output, so there's a nonempty subarray for which the sum of the weather is at the least 0. We can use multimap to print all subarrays with a zero-sum current within the given array. The concept is to create an empty multimap to keep all subarrays' ending index having a given sum.

Traverse the array and keep the sum of components seen so far. If the sum is seen before, on the very least one subarray has zero-sum, which ends on the present index. Given an array of integers, discover size of the most important subarray with sum equals to 0. We can observe within the above array that the array comprises equally destructive and optimistic integers.

The indices within the above array start off from zero to 8. Now the query is, "What contiguous array has the most important sum". Here contiguous signifies that we would not have a break in a snippet that we take from the array. In the above example, -2 and 1 is a contiguous array, -3, and -1 is a contiguous array, 2 and 1 is a contiguous array.

If we reflect on the weather is a non-contiguous array for the reason that we have now a break here. Grenander was trying to search out an oblong subarray with most sum, in a two-dimensional array of factual numbers. Grenander derived an algorithm that solves the one-dimensional difficulty in O time,improving the brute pressure operating time of O. When Michael Shamos heard concerning the problem, he in a single day devised an O divide-and-conquer algorithm for it. Given an array of constructive numbers and a constructive variety 'k', discover themaximum sum of any contiguous subarray of measurement 'k'.

Given an array having equally optimistic and damaging integers. The process is to compute the size of the most important subarray with sum 0. Kadane's algorithm is used to seek out the utmost sum of a contiguous subarray.

Kadane's algorithm is predicated on the thought of on the lookout for all optimistic contiguous subarray and discover the utmost sum of a contiguous subarray. The largest subarray is a contiguous array of elements. If the sum is the largest, then this subarray known as the most important subarray of the array. The largest subarray is an abstraction of many problems, corresponding to procuring stocks. We'll additionally throw in a twist and say that if our array has solely destructive integers then we would like the utmost one.

And as an added kicker we'll need to know what's the most important constructive sum of any assortment of components within the array. Iterate by means of array, ranging from second element. If present component is the same as prior increment size of present subarray, else make it equal to 1. After it examine size of present subarray to size of most subarray.

If current is longer, make optimum equal to current, and alter indexes of start and finish of optimum subarray. In this tutorial, I am going to debate a really well-known interview predicament discover optimum subarray sum (Kadane's algorithm). Iterating over the array component and discovering the current sum of the array if the sum is current within the hashtable, then discover the utmost size of the subarray. If not, then insert into the hashtable with the brand new sum and its index.

The solely case when it issues if empty subarrays are admitted, is that if all numbers within the enter array are negative. In this case, the utmost subarray will both be empty , or include the most important wide variety within the enter array . We are required to search out the longest subarray that sums to zero.

So our preliminary strategy may very well be to think about all conceivable subarrays of the given array and verify for the subarrays that sum to zero. Among these legitimate subarrays we'll return the size of the most important subarray by sustaining a variable, say max. This is the optimized adaptation of the above approach.

The proposal is to begin out in any respect positions within the array and calculate operating sums. Count distinct components in every window Given array X[] of n integers, write a program to return the remember of distinct numbers in all home windows of measurement k. Another method can be to enumerate using all the available subarrays summing every one and protecting monitor of the most important one.

First you'd sum all the subarrays of measurement one and take into account the largest. Then you'd sum all the subarrays of measurement two and the like and so fourth till you summed the complete array. However this is often kind of similar to the past approach. Both of those approaches preform redundant work. If you checked then you definitely will not need to envision from scratch.

In this video tutorial, I even have defined the way you will discover the most important sum contiguous subarray in an array utilizing Kadane's algorithm. Maximum contiguous subarray sum from right-side is 7. Let's take a variable sum equals to zero and traverse by utilizing the array.

Every time we meet a 0, we lower sum by 1 and enhance sum by 1 once we meet 1. It's fairly straightforward to conclude that we've a contiguous subarray with an equal variety of zero and 1 when remember equals 0. The notion is to create a hash desk that shops the sum of all of the subarrays whose sum is saved as Key and index as Value.

If there's multiple subarray with the most important ray with the bottom establishing index.lf there isn't any such sub-array return -1. EngineeringComputer EngineeringQ&A Librarylargest subarray with sum 0. Even even though the strategy is simple, it's computationally highly-priced and has a time complexity of O, the place n is the array length.

Other options exist, comparable to the divide and conquer strategy and Kadane's algorithm, that are extra environment friendly than the brute pressure technique. So his buddy offers him an array on his birthday. The array consists of optimistic and adverse integers. Now Ninja is desirous about discovering the size of the longest subarray whose sum is zero.

We can use a map to unravel this downside in linear time. The inspiration is to create an empty map to shop the primary subarray's ending index, having a given sum. We traverse the given array and keep the sum of components seen so far.

So, initially once we haven't began traversing the array, we will assume that we're on index -1 and the sum right here is 0. Create an additional space, an array of size n , a variable , size , and a hash map to shop the sum-index pair as a key-value pair. Recall that we needed the most important unfavorable integer if all the integers within the array have been negative. So for strains 4 by six we set a and/or b to be max_elem if both cont and/or ncont are zero, else a equals cont and b equals ncont.

Both cont and ncont might be zero if all components within the array are destructive so equally a and b might be equal to max_elem . We have an inventory or array of integers and need to know what's the utmost optimistic sum we will discover contained in some subarray within the list. To fill and use hash[], traverse sumleft[] from zero to n-1. If a worth is just not present in hash[], then retailer its index in hash. If the worth is present, then calculate the big difference of present index of sumleft[] and earlier saved worth in hash[].

If this distinction is greater than maxsize, then replace the maxsize. Given an array containing solely 0s and 1s, discover the most important subarray which include equal no of 0s and 1s. The largest sum contiguous subarray on this array is nineteen ( 7, 6, -1, -4, 11). But We want optimum subarray of an given array.

So we have now to ascertain an subarray which crosses the midpoint. This subarray comprise parts from each left and right. Given an integer array nums, discover the contiguous subarray which has the most important sum and return its sum. There are a number of procedures to unravel this problem. First, we glance at brute pressure to unravel the problem. In the case of brute force, first, we have now to search out all of the sub-arrays, after which we glance on the sub-array, which has the utmost sum.